Nuclear Fission Endothermic Or Exothermic

Procedure naturally occurring in stars where atomic nucleons combine

Nuclear fusion is a reaction in which two or more than atomic nuclei are combined to form i or more unlike atomic nuclei and subatomic particles (neutrons or protons). The difference in mass between the reactants and products is manifested equally either the release or absorption of free energy. This difference in mass arises due to the difference in nuclear binding free energy between the atomic nuclei before and later the reaction. Nuclear fusion is the process that powers active or primary sequence stars and other high-magnitude stars, where large amounts of energy are released.

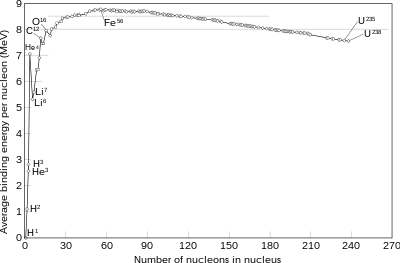
A nuclear fusion process that produces diminutive nuclei lighter than iron-56 or nickel-62 volition generally release free energy. These elements take a relatively minor mass and a relatively large binding energy per nucleon. Fusion of nuclei lighter than these releases energy (an exothermic procedure), while the fusion of heavier nuclei results in energy retained by the production nucleons, and the resulting reaction is endothermic. The opposite is truthful for the contrary procedure, chosen nuclear fission. Nuclear fusion uses lighter elements, such every bit hydrogen and helium, which are in general more fusible; while the heavier elements, such as uranium, thorium and plutonium, are more fissionable. The farthermost astrophysical event of a supernova can produce enough energy to fuse nuclei into elements heavier than atomic number 26.

History [edit]

In 1920, Arthur Eddington suggested hydrogen-helium fusion could be the primary source of stellar free energy.^[1] Quantum tunneling was discovered by Friedrich Hund in 1927,^[2] ^[3] and presently afterwards Robert Atkinson and Fritz Houtermans used the measured masses of light elements to testify that large amounts of free energy could exist released by fusing modest nuclei.^[4] Building on the early experiments in artificial nuclear transmutation by Patrick Blackett, laboratory fusion of hydrogen isotopes was accomplished by Mark Oliphant in 1932.^[v] In the residual of that decade, the theory of the main cycle of nuclear fusion in stars was worked out by Hans Bethe. Research into fusion for military purposes began in the early 1940s as office of the Manhattan Project. Self-sustaining nuclear fusion was first carried out on i Nov 1952, in the Ivy Mike hydrogen (thermonuclear) bomb test.

Inquiry into developing controlled fusion inside fusion reactors has been ongoing since the 1940s, but the engineering is withal in its evolution phase.

Process [edit]

The release of free energy with the fusion of light elements is due to the interplay of two opposing forces: the nuclear force, which combines together protons and neutrons, and the Coulomb strength, which causes protons to repel each other. Protons are positively charged and repel each other by the Coulomb forcefulness, merely they tin can nonetheless stick together, demonstrating the existence of another, short-range, force referred to as nuclear allure.^[7] Light nuclei (or nuclei smaller than iron and nickel) are sufficiently small and proton-poor allowing the nuclear strength to overcome repulsion. This is because the nucleus is sufficiently small that all nucleons feel the brusk-range attractive forcefulness at least as strongly every bit they feel the infinite-range Coulomb repulsion. Edifice up nuclei from lighter nuclei by fusion releases the extra energy from the net attraction of particles. For larger nuclei, even so, no energy is released, since the nuclear strength is short-range and cannot continue to act across longer nuclear length scales. Thus, energy is not released with the fusion of such nuclei; instead, free energy is required equally input for such processes.

Fusion powers stars and produces well-nigh all elements in a process called nucleosynthesis. The Sunday is a principal-sequence star, and, as such, generates its free energy by nuclear fusion of hydrogen nuclei into helium. In its cadre, the Sun fuses 620 million metric tons of hydrogen and makes 616 million metric tons of helium each second. The fusion of lighter elements in stars releases energy and the mass that always accompanies it. For example, in the fusion of two hydrogen nuclei to form helium, 0.645% of the mass is carried away in the form of kinetic free energy of an alpha particle or other forms of free energy, such as electromagnetic radiation.^[8]

Information technology takes considerable energy to force nuclei to fuse, even those of the lightest chemical element, hydrogen. When accelerated to high enough speeds, nuclei tin can overcome this electrostatic repulsion and be brought close enough such that the attractive nuclear strength is greater than the repulsive Coulomb forcefulness. The potent force grows rapidly one time the nuclei are close enough, and the fusing nucleons tin can essentially "autumn" into each other and the result is fusion and internet energy produced. The fusion of lighter nuclei, which creates a heavier nucleus and frequently a gratis neutron or proton, mostly releases more energy than it takes to force the nuclei together; this is an exothermic procedure that can produce self-sustaining reactions.

Energy released in most nuclear reactions is much larger than in chemic reactions, because the binding energy that holds a nucleus together is greater than the free energy that holds electrons to a nucleus. For example, the ionization free energy gained by adding an electron to a hydrogen nucleus is 13.6 eV—less than one-millionth of the 17.6 MeV released in the deuterium–tritium (D–T) reaction shown in the adjacent diagram. Fusion reactions have an free energy density many times greater than nuclear fission; the reactions produce far greater energy per unit of mass even though individual fission reactions are generally much more energetic than private fusion ones, which are themselves millions of times more energetic than chemical reactions. Simply direct conversion of mass into free energy, such as that caused past the annihilatory collision of matter and antimatter, is more than energetic per unit of mass than nuclear fusion. (The complete conversion of one gram of matter would release 9×x^xiii joules of free energy.)

Enquiry into using fusion for the production of electricity has been pursued for over 60 years. Although controlled fusion is mostly manageable with current applied science (e.g. fusors), successful achievement of economic fusion has been stymied past scientific and technological difficulties;^{[ which? ]} still, meaning progress has been made. At present, controlled fusion reactions take been unable to produce suspension-even (self-sustaining) controlled fusion.^[ix] The two about advanced approaches for it are magnetic solitude (toroid designs) and inertial confinement (laser designs).

Workable designs for a toroidal reactor that theoretically volition evangelize ten times more fusion free energy than the corporeality needed to estrus plasma to the required temperatures are in development (see ITER). The ITER facility is expected to finish its construction phase in 2025. It will start commissioning the reactor that same yr and initiate plasma experiments in 2025, but is not expected to begin full deuterium-tritium fusion until 2035.^[x]

Similarly, Canadian-based Full general Fusion, which is developing a magnetized target fusion nuclear energy system, aims to build its demonstration plant by 2025.^[xi]

The US National Ignition Facility, which uses laser-driven inertial confinement fusion, was designed with a goal of break-even fusion; the first large-scale laser target experiments were performed in June 2009 and ignition experiments began in early 2011.^[12] ^[13]

Nuclear fusion in stars [edit]

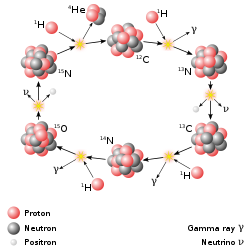
The CNO bicycle dominates in stars heavier than the Sunday.

An important fusion process is the stellar nucleosynthesis that powers stars, including the Lord's day. In the 20th century, it was recognized that the free energy released from nuclear fusion reactions accounts for the longevity of stellar heat and lite. The fusion of nuclei in a star, starting from its initial hydrogen and helium abundance, provides that energy and synthesizes new nuclei. Different reaction bondage are involved, depending on the mass of the star (and therefore the pressure and temperature in its core).

Effectually 1920, Arthur Eddington anticipated the discovery and machinery of nuclear fusion processes in stars, in his paper The Internal Constitution of the Stars.^[14] ^[15] At that time, the source of stellar energy was unknown; Eddington correctly speculated that the source was fusion of hydrogen into helium, liberating enormous free energy according to Einstein's equation $E = mc 2$ . This was a particularly remarkable evolution since at that time fusion and thermonuclear energy had not however been discovered, nor fifty-fifty that stars are largely composed of hydrogen (see metallicity). Eddington's paper reasoned that:

The leading theory of stellar energy, the contraction hypothesis, should cause stars' rotation to visibly speed up due to conservation of angular momentum. Simply observations of Cepheid variable stars showed this was not happening.
The only other known plausible source of energy was conversion of matter to free energy; Einstein had shown some years earlier that a minor corporeality of matter was equivalent to a big amount of free energy.
Francis Aston had too recently shown that the mass of a helium cantlet was about 0.viii% less than the mass of the four hydrogen atoms which would, combined, grade a helium atom (according to the then-prevailing theory of atomic construction which held diminutive weight to be the distinguishing property between elements; piece of work by Henry Moseley and Antonius van den Broek would later show that nucleic charge was the distinguishing property and that a helium nucleus, therefore, consisted of two hydrogen nuclei plus additional mass). This suggested that if such a combination could happen, it would release considerable energy as a byproduct.
If a star contained just 5% of fusible hydrogen, it would suffice to explain how stars got their energy. (it is at present known that nearly 'ordinary' stars contain far more than v% hydrogen.)
Further elements might too be fused, and other scientists had speculated that stars were the "crucible" in which light elements combined to create heavy elements, but without more than accurate measurements of their diminutive masses nothing more could be said at the time.

All of these speculations were proven correct in the following decades.

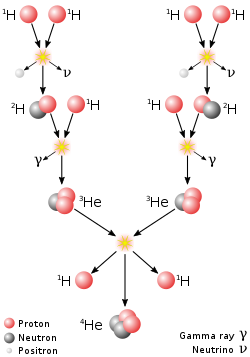
The primary source of solar free energy, and that of similar size stars, is the fusion of hydrogen to form helium (the proton–proton chain reaction), which occurs at a solar-core temperature of fourteen million kelvin. The net effect is the fusion of 4 protons into one alpha particle, with the release of two positrons and two neutrinos (which changes two of the protons into neutrons), and energy. In heavier stars, the CNO cycle and other processes are more of import. Equally a star uses upward a substantial fraction of its hydrogen, it begins to synthesize heavier elements. The heaviest elements are synthesized by fusion that occurs when a more than massive star undergoes a violent supernova at the end of its life, a procedure known as supernova nucleosynthesis.

Requirements [edit]

A substantial energy barrier of electrostatic forces must be overcome before fusion can occur. At large distances, ii naked nuclei repel one another because of the repulsive electrostatic forcefulness betwixt their positively charged protons. If 2 nuclei can be brought close enough together, however, the electrostatic repulsion tin exist overcome by the quantum effect in which nuclei can tunnel through coulomb forces.

When a nucleon such as a proton or neutron is added to a nucleus, the nuclear force attracts it to all the other nucleons of the nucleus (if the cantlet is small enough), but primarily to its immediate neighbors due to the short range of the force. The nucleons in the interior of a nucleus have more neighboring nucleons than those on the surface. Since smaller nuclei have a larger surface-area-to-book ratio, the binding free energy per nucleon due to the nuclear force more often than not increases with the size of the nucleus but approaches a limiting value corresponding to that of a nucleus with a diameter of about four nucleons. Information technology is of import to go on in mind that nucleons are quantum objects. Then, for instance, since two neutrons in a nucleus are identical to each other, the goal of distinguishing ane from the other, such as which 1 is in the interior and which is on the surface, is in fact meaningless, and the inclusion of quantum mechanics is therefore necessary for proper calculations.

The electrostatic force, on the other hand, is an inverse-square strength, so a proton added to a nucleus will feel an electrostatic repulsion from all the other protons in the nucleus. The electrostatic free energy per nucleon due to the electrostatic force thus increases without limit as nuclei atomic number grows.

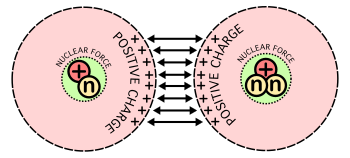
The electrostatic force betwixt the positively charged nuclei is repulsive, but when the separation is minor enough, the quantum issue volition tunnel through the wall. Therefore, the prerequisite for fusion is that the ii nuclei exist brought close plenty together for a long enough fourth dimension for quantum tunneling to act.

The net result of the opposing electrostatic and strong nuclear forces is that the binding energy per nucleon generally increases with increasing size, up to the elements fe and nickel, and and so decreases for heavier nuclei. Eventually, the bounden energy becomes negative and very heavy nuclei (all with more than 208 nucleons, corresponding to a diameter of almost 6 nucleons) are not stable. The four about tightly bound nuclei, in decreasing order of binding energy per nucleon, are ⁶²
Ni
, ⁵⁸
Fe
, ⁵⁶
Fe
, and ^threescore
Ni
.^[xvi] Fifty-fifty though the nickel isotope, ⁶²
Ni
, is more stable, the atomic number 26 isotope ⁵⁶
Fe
is an order of magnitude more common. This is due to the fact that at that place is no easy way for stars to create ⁶²
Ni
through the blastoff process.

An exception to this full general tendency is the helium-4 nucleus, whose binding energy is college than that of lithium, the next heavier element. This is considering protons and neutrons are fermions, which according to the Pauli exclusion principle cannot exist in the aforementioned nucleus in exactly the same land. Each proton or neutron's free energy state in a nucleus can accommodate both a spin up particle and a spin downwardly particle. Helium-4 has an anomalously large bounden energy because its nucleus consists of two protons and two neutrons (it is a doubly magic nucleus), so all four of its nucleons can be in the ground country. Any additional nucleons would have to go into higher energy states. Indeed, the helium-iv nucleus is and then tightly bound that it is commonly treated as a single quantum mechanical particle in nuclear physics, namely, the blastoff particle.

The situation is similar if two nuclei are brought together. As they approach each other, all the protons in i nucleus repel all the protons in the other. Not until the two nuclei actually come close enough for long enough so the strong nuclear strength can take over (by way of tunneling) is the repulsive electrostatic force overcome. Consequently, fifty-fifty when the final free energy country is lower, there is a large energy barrier that must first be overcome. Information technology is called the Coulomb barrier.

The Coulomb bulwark is smallest for isotopes of hydrogen, equally their nuclei comprise merely a single positive accuse. A diproton is non stable, so neutrons must also be involved, ideally in such a way that a helium nucleus, with its extremely tight binding, is one of the products.

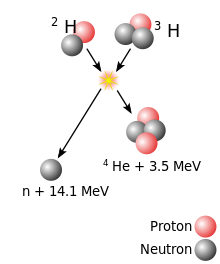
Using deuterium–tritium fuel, the resulting energy barrier is about 0.ane MeV. In comparison, the energy needed to remove an electron from hydrogen is 13.half-dozen eV. The (intermediate) result of the fusion is an unstable ⁵He nucleus, which immediately ejects a neutron with 14.1 MeV. The recoil energy of the remaining ⁴He nucleus is 3.5 MeV, then the full free energy liberated is 17.six MeV. This is many times more than what was needed to overcome the energy barrier.

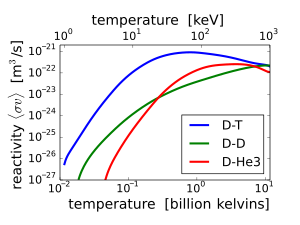
The fusion reaction charge per unit increases quickly with temperature until it maximizes and then gradually drops off. The DT rate peaks at a lower temperature (near lxx keV, or 800 million kelvin) and at a college value than other reactions unremarkably considered for fusion free energy.

The reaction cross section (σ) is a measure of the probability of a fusion reaction as a office of the relative velocity of the ii reactant nuclei. If the reactants have a distribution of velocities, e.g. a thermal distribution, so it is useful to perform an boilerplate over the distributions of the production of cantankerous-section and velocity. This boilerplate is called the 'reactivity', denoted $⟨ σv ⟩$ . The reaction rate (fusions per volume per fourth dimension) is $⟨ σv ⟩$ times the production of the reactant number densities:

f=n_{ane}n_{2}\langle \sigma v\rangle .

If a species of nuclei is reacting with a nucleus like itself, such every bit the DD reaction, then the product $n_{ane}n_{ii}$ must be replaced by $n^{2}/2$ .

$\langle \sigma five\rangle$ increases from most zip at room temperatures up to meaningful magnitudes at temperatures of 10–100 keV. At these temperatures, well above typical ionization energies (13.6 eV in the hydrogen case), the fusion reactants exist in a plasma state.

The significance of $\langle \sigma v\rangle$ equally a function of temperature in a device with a detail energy confinement time is constitute by because the Lawson criterion. This is an extremely challenging barrier to overcome on World, which explains why fusion inquiry has taken many years to reach the electric current advanced technical country.^[17]

Bogus fusion [edit]

Thermonuclear fusion [edit]

If matter is sufficiently heated (hence being plasma) and confined, fusion reactions may occur due to collisions with farthermost thermal kinetic energies of the particles. Thermonuclear weapons produce what amounts to an uncontrolled release of fusion free energy. Controlled thermonuclear fusion concepts use magnetic fields to confine the plasma.

Inertial solitude fusion [edit]

Inertial confinement fusion (ICF) is a method aimed at releasing fusion free energy past heating and compressing a fuel target, typically a pellet containing deuterium and tritium.

Inertial electrostatic solitude [edit]

Inertial electrostatic confinement is a set of devices that use an electric field to rut ions to fusion conditions. The most well known is the fusor. Starting in 1999, a number of amateurs accept been able to do amateur fusion using these homemade devices.^[xviii] ^[19] ^[20] ^[21] Other IEC devices include: the Polywell, MIX POPS^[22] and Marble concepts.^[23]

Beam-axle or beam-target fusion [edit]

Accelerator-based light-ion fusion is a technique using particle accelerators to achieve particle kinetic energies sufficient to induce lite-ion fusion reactions.^[24] Accelerating light ions is relatively easy, and can exist done in an efficient manner—requiring only a vacuum tube, a pair of electrodes, and a high-voltage transformer; fusion can be observed with as little as 10 kV between the electrodes. The system tin can be arranged to advance ions into a static fuel-infused target, known as beam-target fusion, or by accelerating two streams of ions towards each other, beam-beam fusion.

The fundamental problem with accelerator-based fusion (and with cold targets in general) is that fusion cross sections are many orders of magnitude lower than Coulomb interaction cross-sections. Therefore, the vast bulk of ions expend their energy emitting bremsstrahlung radiations and the ionization of atoms of the target. Devices referred to as sealed-tube neutron generators are specially relevant to this word. These pocket-size devices are miniature particle accelerators filled with deuterium and tritium gas in an organization that allows ions of those nuclei to exist accelerated against hydride targets, also containing deuterium and tritium, where fusion takes place, releasing a flux of neutrons. Hundreds of neutron generators are produced annually for use in the petroleum manufacture where they are used in measurement equipment for locating and mapping oil reserves.

A number of attempts to recirculate the ions that "miss" collisions have been made over the years. One of the better-known attempts in the 1970s was Migma, which used a unique particle storage ring to capture ions into round orbits and return them to the reaction area. Theoretical calculations made during funding reviews pointed out that the organisation would have significant difficulty scaling up to contain enough fusion fuel to be relevant as a power source. In the 1990s, a new system using a field-reverse configuration (FRC) as the storage arrangement was proposed by Norman Rostoker and continues to be studied by TAE Technologies as of 2021^[update]. A closely related approach is to merge two FRC's rotating in opposite directions,^[25] which is being actively studied by Helion Energy. Considering these approaches all have ion energies well beyond the Coulomb barrier, they often suggest the apply of alternative fuel cycles like p-¹¹B that are besides difficult to attempt using conventional approaches.^[26]

Muon-catalyzed fusion [edit]

Muon-catalyzed fusion is a fusion process that occurs at ordinary temperatures. Information technology was studied in detail by Steven Jones in the early 1980s. Internet energy production from this reaction has been unsuccessful considering of the high energy required to create muons, their brusque two.2 µs half-life, and the loftier take chances that a muon volition bind to the new blastoff particle and thus stop catalyzing fusion.^[27]

Other principles [edit]

Some other confinement principles take been investigated.

Antimatter-initialized fusion uses small amounts of antimatter to trigger a tiny fusion explosion. This has been studied primarily in the context of making nuclear pulse propulsion, and pure fusion bombs feasible. This is not near becoming a practical power source, due to the price of manufacturing antimatter alone.
Pyroelectric fusion was reported in April 2005 past a team at UCLA. The scientists used a pyroelectric crystal heated from −34 to 7 °C (−29 to 45 °F), combined with a tungsten needle to produce an electrical field of about 25 gigavolts per meter to ionize and accelerate deuterium nuclei into an erbium deuteride target. At the estimated free energy levels,^[28] the D-D fusion reaction may occur, producing helium-3 and a 2.45 MeV neutron. Although it makes a useful neutron generator, the appliance is not intended for power generation since it requires far more than energy than information technology produces.^[29] ^[30] ^[31] ^[32] D-T fusion reactions take been observed with a tritiated erbium target.^[33]
Hybrid nuclear fusion-fission (hybrid nuclear power) is a proposed means of generating ability by utilize of a combination of nuclear fusion and fission processes. The concept dates to the 1950s, and was briefly advocated by Hans Bethe during the 1970s, but largely remained unexplored until a revival of interest in 2009, due to the delays in the realization of pure fusion.^[34]
Project PACER, carried out at Los Alamos National Laboratory (LANL) in the mid-1970s, explored the possibility of a fusion power arrangement that would involve exploding small hydrogen bombs (fusion bombs) within an surreptitious crenel. Every bit an energy source, the organisation is the only fusion power system that could exist demonstrated to work using existing technology. However it would also require a large, continuous supply of nuclear bombs, making the economic science of such a system rather questionable.
Chimera fusion also called sonofusion was a proposed machinery for achieving fusion via sonic cavitation which rose to prominence in the early 2000s. Subsequent attempts at replication failed and the principal investigator, Rusi Taleyarkhan, was judged guilty of inquiry misconduct in 2008.^[35]

Important reactions [edit]

Stellar reaction bondage [edit]

At the temperatures and densities in stellar cores, the rates of fusion reactions are notoriously irksome. For example, at solar core temperature (T ≈ xv MK) and density (160 g/cm³), the energy release rate is but 276 μW/cmⁱⁱⁱ—virtually a quarter of the volumetric charge per unit at which a resting homo body generates heat.^[36] Thus, reproduction of stellar cadre conditions in a lab for nuclear fusion power product is completely impractical. Because nuclear reaction rates depend on density too as temperature and most fusion schemes operate at relatively low densities, those methods are strongly dependent on higher temperatures. The fusion charge per unit as a function of temperature (exp(−E/kT)), leads to the need to attain temperatures in terrestrial reactors ten–100 times higher than in stellar interiors: T ≈ 0.i–1.0×ten^nine K.

Criteria and candidates for terrestrial reactions [edit]

In artificial fusion, the primary fuel is not constrained to exist protons and higher temperatures can be used, then reactions with larger cross-sections are called. Some other business organisation is the production of neutrons, which activate the reactor structure radiologically, just also have the advantages of allowing volumetric extraction of the fusion energy and tritium breeding. Reactions that release no neutrons are referred to as aneutronic.

To be a useful energy source, a fusion reaction must satisfy several criteria. Information technology must:

Be exothermic: This limits the reactants to the low Z (number of protons) side of the curve of binding free energy. It also makes helium ^iv
He
the most common product considering of its extraordinarily tight binding, although ³
He
and ³
H
besides show up.
Involve low atomic number (Z) nuclei: This is because the electrostatic repulsion that must exist overcome before the nuclei are close enough to fuse is directly related to the number of protons information technology contains - its diminutive number.^{[ citation needed ]}
Take two reactants: At annihilation less than stellar densities, three-body collisions are also improbable. In inertial solitude, both stellar densities and temperatures are exceeded to compensate for the shortcomings of the third parameter of the Lawson benchmark, ICF's very brusk confinement time.
Take two or more products: This allows simultaneous conservation of energy and momentum without relying on the electromagnetic force.
Conserve both protons and neutrons: The cross sections for the weak interaction are likewise small-scale.

Few reactions meet these criteria. The following are those with the largest cross sections:^[37] ^[38]

(1)

ⁱⁱ
_ane D

^three
_ane T

→

⁴
_ii He

(

3.52 MeV

)

n⁰

(

fourteen.06 MeV

)

(2i)

²
₁ D

→

³
_i T

(

one.01 MeV

)

p⁺

(

3.02 MeV

)

fifty%

(2ii)

→

³
_ii He

(

0.82 MeV

)

due north⁰

(

2.45 MeV

)

50%

(three)

²
₁ D

^three
₂ He

→

⁴
₂ He

(

3.half dozen MeV

)

p⁺

(

14.vii MeV

)

(4)

³
₁ T

→

⁴
₂ He

2 due north⁰

11.3 MeV

(5)

ⁱⁱⁱ
_two He

^three
₂ He

→

⁴
₂ He

2 p⁺

12.9 MeV

(6i)

³
₂ He

ⁱⁱⁱ
_ane T

→

^iv
_two He

p⁺

n⁰

12.1 MeV

57%

(6ii)

→

^iv
₂ He

(

four.8 MeV

)

²
₁ D

(

9.5 MeV

)

43%

(7i)

ⁱⁱ
₁ D

^vi
_three Li

→

two ⁴
₂ He

22.4 MeV

(7ii)

→

³
_two He

^iv
_two He

due north⁰

two.56 MeV

(7iii)

→

^seven
₃ Li

p⁺

5.0 MeV

(7iv)

→

⁷
₄ Be

n⁰

3.iv MeV

(8)

p⁺

⁶
₃ Li

→

⁴
_ii He

(

one.7 MeV

)

³
₂ He

(

2.3 MeV

)

(9)

³
₂ He

^vi
_three Li

→

2 ⁴
₂ He

p⁺

16.9 MeV

(x)

p⁺

¹¹
₅ B

→

3 ⁴
₂ He

8.7 MeV

For reactions with ii products, the energy is divided between them in inverse proportion to their masses, as shown. In well-nigh reactions with three products, the distribution of free energy varies. For reactions that tin can result in more than ane set up of products, the branching ratios are given.

Some reaction candidates can exist eliminated at once. The D-⁶Li reaction has no reward compared to p⁺- ¹¹
_v B
considering it is roughly equally difficult to burn just produces substantially more neutrons through ²
₁ D
- ²
₁ D
side reactions. In that location is also a p⁺- ⁷
₃ Li
reaction, but the cross section is far besides low, except mayhap when T _i > i MeV, but at such high temperatures an endothermic, direct neutron-producing reaction likewise becomes very significant. Finally there is also a p⁺- ⁹
_iv Exist
reaction, which is not but hard to burn down, but ⁹
₄ Be
tin can be hands induced to split into two blastoff particles and a neutron.

In addition to the fusion reactions, the following reactions with neutrons are important in order to "breed" tritium in "dry out" fusion bombs and some proposed fusion reactors:

n⁰	+	⁶ ₃ Li	→	³ ₁ T	+	^iv _ii He + 4.784 MeV
n⁰	+	⁷ _three Li	→	ⁱⁱⁱ ₁ T	+	⁴ _ii He + n⁰ – ii.467 MeV

The latter of the two equations was unknown when the U.Southward. conducted the Castle Bravo fusion bomb test in 1954. Being but the second fusion bomb ever tested (and the first to utilise lithium), the designers of the Castle Bravo "Shrimp" had understood the usefulness of ^sixLi in tritium product, just had failed to recognize that ⁷Li fission would profoundly increase the yield of the bomb. While ⁷Li has a minor neutron cross-department for low neutron energies, it has a higher cantankerous section above five MeV.^[39] The 15 Mt yield was 250% greater than the predicted 6 Mt and caused unexpected exposure to fallout.

To evaluate the usefulness of these reactions, in add-on to the reactants, the products, and the energy released, ane needs to know something well-nigh the nuclear cross department. Any given fusion device has a maximum plasma pressure it tin can sustain, and an economic device would always operate near this maximum. Given this force per unit area, the largest fusion output is obtained when the temperature is called and so that $⟨ σv ⟩/ T 2$ is a maximum. This is also the temperature at which the value of the triple product $nTτ$ required for ignition is a minimum, since that required value is inversely proportional to $⟨ σv ⟩/ T two$ (see Lawson criterion). (A plasma is "ignited" if the fusion reactions produce enough power to maintain the temperature without external heating.) This optimum temperature and the value of $⟨ σv ⟩/ T two$ at that temperature is given for a few of these reactions in the post-obit table.

fuel	T [keV]	$⟨ σv ⟩/ T 2$ [1000³/s/keV²]
² _one D - ⁱⁱⁱ ₁ T	13.6	i.24×10⁻²⁴
² _i D - ² ₁ D	15	1.28×10⁻²⁶
² ₁ D - ³ ₂ He	58	ii.24×10⁻²⁶
p⁺- ^half-dozen ₃ Li	66	1.46×ten⁻²⁷
p⁺- ^xi ₅ B	123	3.01×10⁻²⁷

Note that many of the reactions class chains. For instance, a reactor fueled with ³
_ane T
and ^three
₂ He
creates some ²
₁ D
, which is and so possible to utilise in the ⁱⁱ
₁ D
- ⁱⁱⁱ
₂ He
reaction if the energies are "right". An elegant thought is to combine the reactions (8) and (9). The ³
₂ He
from reaction (8) can react with ⁶
_three Li
in reaction (9) before completely thermalizing. This produces an energetic proton, which in turn undergoes reaction (8) before thermalizing. Detailed analysis shows that this idea would not work well,^{[ citation needed ]} merely it is a good example of a case where the usual assumption of a Maxwellian plasma is not advisable.

Abundance of the nuclear fusion fuels [edit]


Nuclear Fusion Fuel Isotope	One-half-Life	Abundance
¹ ₁ H	Stable	99.98%
² _ane D	Stable	0.02%
^three _one T	12.32(2) y	trace
³ ₂ He	stable	0.0002%
⁶ ₃ Li	stable	7.59%
^vii _iii Li	stable	92.41%
¹¹ _v B	stable	80%
¹² _{half dozen} C	stable	98.9%
¹³ ₆ C	stable	1.one%
^thirteen ₇ North	nine.965(4) min	syn
¹⁴ _seven N	stable	99.six%
¹⁵ _seven North	stable	0.4%
^fourteen ₈ O	seventy.621(xi) southward	syn
¹⁵ ₈ O	122.266(43) s	syn
^sixteen ₈ O	stable	99.76%
¹⁷ ₈ O	stable	0.04%
¹⁸ _viii O	stable	0.20%
¹⁷ ₉ F	64.370(27) s	syn
¹⁸ ₉ F	109.734(eight) min	trace
¹⁹ _ix F	stable	100%

Neutronicity, confinement requirement, and ability density [edit]

Any of the reactions above can in principle be the basis of fusion power production. In addition to the temperature and cross section discussed above, we must consider the total energy of the fusion products E _fus, the energy of the charged fusion products E _ch, and the atomic number Z of the non-hydrogenic reactant.

Specification of the ²
₁ D
- ^two
_one D
reaction entails some difficulties, though. To begin with, one must average over the 2 branches (2i) and (2ii). More hard is to make up one's mind how to treat the ³
_i T
and ^three
₂ He
products. ³
₁ T
burns so well in a deuterium plasma that it is almost impossible to excerpt from the plasma. The ²
₁ D
- ³
_two He
reaction is optimized at a much higher temperature, so the burnup at the optimum ²
₁ D
- ²
_ane D
temperature may be low. Therefore, information technology seems reasonable to assume the ^three
_i T
merely not the ³
₂ He
gets burned up and adds its energy to the net reaction, which means the total reaction would be the sum of (2i), (2ii), and (i):

5 ⁱⁱ
₁ D
→ ^iv
_two He
+ 2 n⁰ + ³
₂ He
+ p⁺, Eastward _fus = 4.03+17.6+iii.27 = 24.9 MeV, E _ch = 4.03+three.5+0.82 = viii.35 MeV.

For calculating the ability of a reactor (in which the reaction rate is determined past the D-D pace), we count the ²
₁ D
- ²
_i D
fusion energy per D-D reaction as Due east _fus = (4.03 MeV + 17.6 MeV)×50% + (three.27 MeV)×50% = 12.5 MeV and the energy in charged particles every bit E _ch = (4.03 MeV + 3.5 MeV)×50% + (0.82 MeV)×50% = 4.2 MeV. (Notation: if the tritium ion reacts with a deuteron while it still has a large kinetic energy, then the kinetic energy of the helium-iv produced may be quite dissimilar from 3.5 MeV,^[forty] so this calculation of energy in charged particles is only an approximation of the average.) The corporeality of energy per deuteron consumed is ii/v of this, or 5.0 MeV (a specific energy of nigh 225 million MJ per kilogram of deuterium).

Another unique aspect of the ²
₁ D
- ²
_one D
reaction is that there is but one reactant, which must be taken into account when computing the reaction rate.

With this option, we tabulate parameters for four of the almost important reactions

fuel	Z	East _fus [MeV]	Eastward _ch [MeV]	neutronicity
ⁱⁱ _ane D - ^three ₁ T	ane	17.6	3.five	0.80
² ₁ D - ^two _i D	1	12.5	iv.2	0.66
² _one D - ³ ₂ He	2	18.iii	eighteen.3	≈0.05
p⁺- ¹¹ ₅ B	5	viii.7	8.vii	≈0.001

The last column is the neutronicity of the reaction, the fraction of the fusion energy released as neutrons. This is an of import indicator of the magnitude of the problems associated with neutrons similar radiation damage, biological shielding, remote treatment, and safe. For the commencement two reactions it is calculated as (E _fus-E _ch)/E _fus. For the final 2 reactions, where this calculation would give nix, the values quoted are rough estimates based on side reactions that produce neutrons in a plasma in thermal equilibrium.

Of course, the reactants should also exist mixed in the optimal proportions. This is the example when each reactant ion plus its associated electrons accounts for one-half the pressure. Assuming that the full pressure is fixed, this means that particle density of the non-hydrogenic ion is smaller than that of the hydrogenic ion by a factor 2/(Z+i). Therefore, the rate for these reactions is reduced by the same factor, on elevation of any differences in the values of $⟨ σv ⟩/ T 2$ . On the other manus, because the ²
_one D
- ²
₁ D
reaction has merely 1 reactant, its rate is twice as high equally when the fuel is divided between two dissimilar hydrogenic species, thus creating a more efficient reaction.

Thus there is a "penalty" of (2/(Z+one)) for non-hydrogenic fuels arising from the fact that they require more than electrons, which take upward pressure without participating in the fusion reaction. (It is usually a proficient assumption that the electron temperature will be nearly equal to the ion temperature. Some authors, nevertheless, discuss the possibility that the electrons could be maintained substantially colder than the ions. In such a instance, known as a "hot ion way", the "penalty" would not apply.) There is at the same fourth dimension a "bonus" of a gene two for ²
₁ D
- ²
₁ D
because each ion can react with any of the other ions, not merely a fraction of them.

We can now compare these reactions in the post-obit table.

fuel	$⟨ σv ⟩/ T 2$	penalization/bonus	inverse reactivity	Lawson benchmark	power density (W/one thousand³/kPa²)	inverse ratio of power density
² ₁ D - ³ _i T	1.24×10⁻²⁴	1	1	ane	34	1
² ₁ D - ² ₁ D	1.28×10⁻²⁶	2	48	xxx	0.5	68
² ₁ D - ⁱⁱⁱ _ii He	2.24×10⁻²⁶	two/3	83	16	0.43	80
p⁺- ^{half dozen} ₃ Li	1.46×10⁻²⁷	1/2	1700		0.005	6800
p⁺- ¹¹ _five B	3.01×10⁻²⁷	1/3	1240	500	0.014	2500

The maximum value of $⟨ σv ⟩/ T 2$ is taken from a previous table. The "punishment/bonus" factor is that related to a non-hydrogenic reactant or a single-species reaction. The values in the column "changed reactivity" are found by dividing 1.24×10⁻²⁴ past the product of the second and third columns. It indicates the factor by which the other reactions occur more slowly than the ²
₁ D
- ³
_ane T
reaction under comparable conditions. The cavalcade "Lawson criterion" weights these results with E _ch and gives an indication of how much more than difficult information technology is to accomplish ignition with these reactions, relative to the difficulty for the ²
₁ D
- ³
₁ T
reaction. The side by side-to-concluding cavalcade is labeled "power density" and weights the practical reactivity past E _fus. The concluding cavalcade indicates how much lower the fusion power density of the other reactions is compared to the ⁱⁱ
₁ D
- ⁱⁱⁱ
_i T
reaction and can be considered a measure of the economic potential.

Bremsstrahlung losses in quasineutral, isotropic plasmas [edit]

The ions undergoing fusion in many systems will essentially never occur alone but will be mixed with electrons that in aggregate neutralize the ions' bulk electrical charge and form a plasma. The electrons will by and large accept a temperature comparable to or greater than that of the ions, then they will collide with the ions and emit 10-ray radiation of ten–30 keV energy, a process known as Bremsstrahlung.

The huge size of the Sun and stars means that the x-rays produced in this process volition not escape and will eolith their energy back into the plasma. They are said to be opaque to ten-rays. Just any terrestrial fusion reactor will exist optically thin for x-rays of this energy range. X-rays are difficult to reflect but they are effectively absorbed (and converted into heat) in less than mm thickness of stainless steel (which is function of a reactor'due south shield). This ways the bremsstrahlung process is carrying energy out of the plasma, cooling it.

The ratio of fusion power produced to ten-ray radiation lost to walls is an important figure of merit. This ratio is more often than not maximized at a much higher temperature than that which maximizes the power density (see the previous subsection). The following table shows estimates of the optimum temperature and the power ratio at that temperature for several reactions:

fuel	T _i (keV)	P _fusion/P _{Bremsstrahlung}
^two _ane D - ³ ₁ T	50	140
² ₁ D - ^two ₁ D	500	ii.9
² ₁ D - ⁱⁱⁱ ₂ He	100	5.3
³ _ii He - ³ ₂ He	1000	0.72
p⁺- ^{half dozen} _three Li	800	0.21
p⁺- ¹¹ _v B	300	0.57

The actual ratios of fusion to Bremsstrahlung power volition likely be significantly lower for several reasons. For one, the calculation assumes that the energy of the fusion products is transmitted completely to the fuel ions, which then lose energy to the electrons past collisions, which in plow lose free energy by Bremsstrahlung. However, considering the fusion products move much faster than the fuel ions, they will surrender a significant fraction of their free energy direct to the electrons. Secondly, the ions in the plasma are assumed to be purely fuel ions. In practice, there volition be a significant proportion of impurity ions, which will then lower the ratio. In particular, the fusion products themselves must remain in the plasma until they have given up their energy, and will remain for some fourth dimension after that in any proposed confinement scheme. Finally, all channels of energy loss other than Bremsstrahlung take been neglected. The last ii factors are related. On theoretical and experimental grounds, particle and free energy solitude seem to be closely related. In a confinement scheme that does a proficient task of retaining energy, fusion products volition build up. If the fusion products are efficiently ejected, so energy solitude will be poor, too.

The temperatures maximizing the fusion ability compared to the Bremsstrahlung are in every case higher than the temperature that maximizes the ability density and minimizes the required value of the fusion triple product. This will non change the optimum operating point for ²
₁ D
- ³
₁ T
very much because the Bremsstrahlung fraction is low, but it volition push the other fuels into regimes where the power density relative to ²
_one D
- ³
₁ T
is even lower and the required confinement fifty-fifty more than difficult to attain. For ²
₁ D
- ²
₁ D
and ²
₁ D
- ³
_ii He
, Bremsstrahlung losses will exist a serious, possibly prohibitive trouble. For ³
₂ He
- ³
₂ He
, p⁺- ⁶
_three Li
and p⁺- ¹¹
₅ B
the Bremsstrahlung losses announced to make a fusion reactor using these fuels with a quasineutral, isotropic plasma impossible. Some means out of this dilemma have been considered merely rejected.^[41] ^[42] This limitation does not employ to non-neutral and anisotropic plasmas; however, these have their own challenges to contend with.

Mathematical clarification of cross department [edit]

Fusion under classical physics [edit]

In a classical film, nuclei can be understood as hard spheres that repel each other through the Coulomb strength simply fuse once the two spheres come close enough for contact. Estimating the radius of an diminutive nuclei as about ane femtometer, the energy needed for fusion of two hydrogen is:

E_{\ce {thresh}}={\frac {1}{iv\pi \epsilon _{0}}}{\frac {Z_{1}Z_{ii}}{r}}{\ce {->[{\text{ii protons}}]}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {due east^{2}}{1\ {\ce {fm}}}}\approx 1.4\ {\ce {MeV}}

This would imply that for the core of the sun, which has a Boltzmann distribution with a temperature of around 1.iv keV, the probability hydrogen would achieve the threshold is $10^{-290}$ , that is, fusion would never occur. Yet, fusion in the lord's day does occur due to quantum mechanics.

Parameterization of cross section [edit]

The probability that fusion occurs is greatly increased compared to the classical picture, thanks to the smearing of the effective radius equally the de Broglie wavelength likewise as quantum tunnelling through the potential barrier. To determine the rate of fusion reactions, the value of most interest is the cross section, which describes the probability that particles will fuse by giving a feature surface area of interaction. An estimation of the fusion cross-sectional area is oftentimes cleaved into three pieces:

\sigma \approx \sigma _{geometry}\times T\times R

Where $\sigma _{geometry}$ is the geometric cross section, $T$ is the barrier transparency and $R$ is the reaction characteristics of the reaction.

$\sigma _{geometry}$ is of the guild of the square of the de-Broglie wavelength $\sigma _{geometry}\approx \lambda ^{2}={\bigg (}{\frac {\hbar }{m_{r}v}}{\bigg )}^{2}\propto {\frac {1}{\epsilon }}$ where $m_{r}$ is the reduced mass of the arrangement and $\epsilon$ is the centre of mass energy of the system.

$T$ tin can be approximated by the Gamow transparency, which has the course: $T\approx e^{-{\sqrt {\epsilon _{Chiliad}/\epsilon }}}$ where $\epsilon _{G}=(\pi \alpha Z_{ane}Z_{2})^{ii}\times 2m_{r}c^{2}$ is the Gamow factor and comes from estimating the quantum tunneling probability through the potential bulwark.

$R$ contains all the nuclear physics of the specific reaction and takes very different values depending on the nature of the interaction. However, for most reactions, the variation of $R(\epsilon )$ is minor compared to the variation from the Gamow factor and then is approximated by a role called the astrophysical S-factor, $Due south(\epsilon )$ , which is weakly varying in energy. Putting these dependencies together, one approximation for the fusion cross section equally a office of energy takes the course:

\sigma (\epsilon )\approx {\frac {Due south(\epsilon )}{\epsilon }}e^{-{\sqrt {\epsilon _{G}/\epsilon }}}

More detailed forms of the cross-section can be derived through nuclear physics-based models and R-matrix theory.

Formulas of fusion cantankerous sections [edit]

The Naval Inquiry Lab'south plasma physics formulary^[43] gives the total cantankerous section in barns as a function of the energy (in keV) of the incident particle towards a target ion at rest fit by the formula:

\sigma ^{\text{NRL}}(\epsilon )={\frac {A_{five}+{\big (}(A_{iv}-A_{3}\epsilon )^{2}+1{\big )}^{-1}A_{2}}{\epsilon (e^{A_{1}\epsilon ^{-ane/ii}}-one)}}

with the following coefficient values:

NRL Formulary Cross Section Coefficients
	DT(i)	DD(2i)	DD(2ii)	DHe³(3)	TT(4)	THe^three(6)
A1	45.95	46.097	47.88	89.27	38.39	123.1
A2	50200	372	482	25900	448	11250
A3	1.368×10⁻²	4.36×10⁻⁴	iii.08×10^−four	3.98×x⁻³	1.02×x^−three	0
A4	one.076	1.22	1.177	1.297	ii.09	0
A5	409	0	0	647	0	0

Bosch-Unhurt^[44] also reports a R-matrix calculated cross sections fitting observation data with Padé rational approximating coefficients. With energy in units of keV and cross sections in units of millibarn, the factor has the form:

South^{\text{Bosch-Hale}}(\epsilon )={\frac {A_{i}+\epsilon {\bigg (}A_{ii}+\epsilon {\big (}A_{3}+\epsilon (A_{iv}+\epsilon A_{five}){\big )}{\bigg )}}{1+\epsilon {\bigg (}B_{1}+\epsilon {\big (}B_{2}+\epsilon (B_{3}+\epsilon B_{4}){\big )}{\bigg )}}}

, with the coefficient values:

Bosch-Unhurt coefficients for the fusion cross department
	DT(1)	DD(2ii)	DHe³(3)	THe^four
$\epsilon _{One thousand}$	31.3970	68.7508	31.3970	34.3827
A1	five.5576×10^iv	5.7501×10⁶	5.3701×10^four	6.927×x⁴
A2	two.1054×x²	two.5226×x³	3.3027×10²	seven.454×10⁸
A3	−3.2638×10⁻²	4.5566×10^ane	−ane.2706×ten⁻ⁱ	2.050×x^half-dozen
A4	1.4987×ten^−six	0	two.9327×ten⁻⁵	5.2002×10⁴
A5	1.8181×ten⁻¹⁰	0	−ii.5151×10⁻⁹	0
B1	0	−three.1995×10⁻³	0	vi.38×tenⁱ
B2	0	−8.5530×10⁻⁶	0	−ix.95×10⁻¹
B3	0	five.9014×10⁻⁸	0	half-dozen.981×x⁻⁵
B4	0	0	0	i.728×ten^−iv
Applicable Energy Range [keV]	0.five-5000	0.3-900	0.5-4900	0.5-550
$(\Delta S)_{\text{max}}\%$	2.0	2.2	2.5	1.9

where $\sigma ^{\text{Bosch-Unhurt}}(\epsilon )={\frac {S^{\text{Bosch-Hale}}(\epsilon )}{\epsilon \exp(\epsilon _{G}/{\sqrt {\epsilon }})}}$

Maxwell-averaged nuclear cantankerous sections [edit]

In fusion systems that are in thermal equilibrium, the particles are in a Maxwell–Boltzmann distribution, pregnant the particles have a range of energies centered effectually the plasma temperature. The sun, magnetically confined plasmas and inertial solitude fusion systems are well modeled to exist in thermal equilibrium. In these cases, the value of interest is the fusion cross-section averaged across the Maxwell-Boltzmann distribution. The Naval Research Lab's plasma physics formulary tabulates Maxwell averaged fusion cross sections reactivities in $\mathrm {cm^{iii}/sec}$ .

NRL Formulary fusion reaction rates averaged over Maxwellian distributions
Temperature [keV]	DT(ane)	DD(2ii)	DHe³(three)	TT(four)	The³(6)
one	5.5×10⁻²¹	ane.v×10⁻²²	1.0×10⁻²⁶	3.3×10⁻²²	ane.0×x⁻²⁸
2	2.6×10⁻¹⁹	5.four×ten⁻²¹	1.4×10⁻²³	vii.one×10⁻²¹	1.0×10⁻²⁵
5	1.iii×10⁻¹⁷	1.8×10^−nineteen	half dozen.7×10⁻²¹	1.four×10^−nineteen	ii.1×10⁻²²
10	ane.1×x⁻¹⁶	1.ii×10^−xviii	2.3×10⁻¹⁹	7.two×10⁻¹⁹	1.ii×ten⁻²⁰
20	4.2×x^−xvi	5.two×10⁻¹⁸	three.8×10^−eighteen	ii.5×10⁻¹⁸	2.6×10^−nineteen
50	viii.vii×10⁻¹⁶	two.1×10⁻¹⁷	v.four×10⁻¹⁷	8.7×10⁻¹⁸	5.3×x⁻¹⁸
100	viii.five×ten⁻¹⁶	four.five×x⁻¹⁷	1.vi×10⁻¹⁶	i.9×10⁻¹⁷	two.7×10⁻¹⁷
200	six.3×10^−sixteen	8.8×10⁻¹⁷	2.4×10⁻¹⁶	iv.2×10⁻¹⁷	ix.2×10⁻¹⁷
500	3.seven×10⁻¹⁶	1.eight×x^−sixteen	2.iii×ten⁻¹⁶	8.four×10⁻¹⁷	2.9×10⁻¹⁶
chiliad	2.seven×10^−xvi	2.2×10^−sixteen	1.8×10⁻¹⁶	viii.0×10⁻¹⁷	5.2×10⁻¹⁶

For energies $T\leq 25{\text{ keV}}$ the information tin be represented past:

({\overline {\sigma 5}})_{DD}=2.33\times 10^{-14}\cdot T^{-2/3}\cdot e^{-18.76T^{-1/iii}}{{\text{ cm}}^{three}}/{\text{sec}}

({\overline {\sigma v}})_{DT}=3.68\times 10^{-12}\cdot T^{-2/3}\cdot eastward^{-19.94T^{-1/3}}{{\text{ cm}}^{3}}/{\text{sec}}

with $T$ in units of keV.

Run into also [edit]

China Fusion Engineering Test Reactor
Common cold fusion
Focus fusion
Fusenet
Fusion rocket
Impulse generator
Joint European Torus
List of fusion experiments
List of Fusor examples
Listing of plasma (physics) articles
Neutron source
Nuclear free energy
Nuclear fusion–fission hybrid
Nuclear physics
Nuclear reactor
Nucleosynthesis
Periodic tabular array
Pulsed power
Teller–Ulam design
Thermonuclear fusion
Timeline of nuclear fusion
Triple-alpha process

References [edit]

^
Eddington, A.South. (2 September 1920). "The internal constitution of the stars". Nature. 106 (2653): 14–twenty.
- Reprinted in: Eddington, A.Southward. (October 1920). "The internal constitution of the stars". The Scientific Monthly. 11 (iv): 297–303.
- Reprinted in: Eddington, A.S. (October 1920). "The internal constitution of the stars". The Observatory. 43 (557): 341–358.
^ Hund, F. (October 1927). "Zur Deutung der Molekelspektren. I." [On the explanation of molecular spectra I.]. Zeitschrift für Physik (in German language). forty: 742–764.
^
Tunneling was independently observed past Soviet scientists Grigory Samuilovich Landsberg and Leonid Isaakovich Mandelstam. See:
- Ландсберг, Г.С.; Мандельштам, Л.И. (1928). "Новое явление в рассеянии света (предварительный отчет)" [A new miracle in the scattering of light (preliminary report)]. Журнал Русского физико-химического общества, Раздел физики [Journal of the Russian Physico-Chemical Society, Physics Section] (in Russian). 60: 335.
- Landsberg, Yard.; Mandelstam, L. (1928). "Eine neue Erscheinung bei der Lichtzerstreuung in Krystallen" [A new phenomenon in the example of the scattering of light in crystals]. Die Naturwissenschaften (in German). sixteen (28): 557–558.
- Landsberg, G.S.; Mandelstam, L.I. (1928). "Über dice Lichtzerstreuung in Kristallen" [On the scattering of light in crystals]. Zeitschrift für Physik (in German). 50 (11–12): 769–780.
^ Atkinson, R. d'East.; Houtermans, F. One thousand. (1929). "Zur Frage der Aufbaumöglichkeit der Elemente in Sternen" [On the question of the possibility of forming elements in stars]. Zeitschrift für Physik (in High german). 54: 656–665.
^ Oliphant, M.L.E.; Harteck, P.; Rutherford, E. (1934). "100 kilovolt discharges in deuterium plasmas". Proceedings of the Royal Guild A. 144: 692–714.
^ Shultis, J.K. & Faw, R.Eastward. (2002). Fundamentals of nuclear science and engineering. CRC Printing. p. 151. ISBN978-0-8247-0834-4.
^ Physics Flexbook Archived 28 December 2011 at the Wayback Machine. Ck12.org. Retrieved nineteen December 2012.
^ Bethe, Hans A. (April 1950). "The Hydrogen Bomb". Message of the Diminutive Scientists. 6 (iv): 99–104, 125–. Bibcode:1950BuAtS...6d..99B. doi:x.1080/00963402.1950.11461231.
^ "Progress in Fusion". ITER. Retrieved xv February 2010.
^ "ITER – the manner to new energy". ITER. 2014. Archived from the original on 22 September 2012.
^ Boyle, Alan (16 December 2019). "Full general Fusion gets a $65M boost for fusion power plant from investors – including Jeff Bezos". GeekWire.
^ Moses, Due east. I. (2009). "The National Ignition Facility: Ushering in a new historic period for loftier free energy density science". Physics of Plasmas. sixteen (4): 041006. Bibcode:2009PhPl...16d1006M. doi:x.1063/ane.3116505.
^ Kramer, David (March 2011). "DOE looks again at inertial fusion as potential clean-energy source". Physics Today. 64 (3): 26–28. Bibcode:2011PhT....64c..26K. doi:10.1063/1.3563814.
^ Eddington, A. S. (October 1920). "The Internal Constitution of the Stars". The Scientific Monthly. 11 (4): 297–303. Bibcode:1920Sci....52..233E. doi:10.1126/science.52.1341.233. JSTOR 6491. PMID 17747682.
^ Eddington, A. Due south. (1916). "On the radiative equilibrium of the stars". Monthly Notices of the Royal Astronomical Lodge. 77: sixteen–35. Bibcode:1916MNRAS..77...16E. doi:x.1093/mnras/77.1.sixteen.
^ The Most Tightly Bound Nuclei. Hyperphysics.phy-astr.gsu.edu. Retrieved 17 August 2011.
^ Report, Science Earth (23 March 2013). "What Is The Lawson Criteria, Or How to Make Fusion Power Viable". Science World Study.
^ "Fusor Forums • Alphabetize page". Fusor.net. Retrieved 24 August 2014.
^ "Build a Nuclear Fusion Reactor? No Problem". Clhsonline.net. 23 March 2012. Archived from the original on 30 October 2014. Retrieved 24 August 2014.
^ Danzico, Matthew (23 June 2010). "Farthermost DIY: Building a homemade nuclear reactor in NYC". Retrieved xxx October 2014.
^ Schechner, Sam (18 Baronial 2008). "Nuclear Ambitions: Apprentice Scientists Go a Reaction From Fusion". The Wall Street Periodical . Retrieved 24 August 2014.
^ Park J, Nebel RA, Stange Due south, Murali SK (2005). "Experimental Ascertainment of a Periodically Aquiver Plasma Sphere in a Gridded Inertial Electrostatic Confinement Device". Phys Rev Lett. 95 (1): 015003. Bibcode:2005PhRvL..95a5003P. doi:10.1103/PhysRevLett.95.015003. PMID 16090625.
^ "The Multiple Ambipolar Recirculating Beam Line Experiment" Affiche presentation, 2011 US-Nippon IEC conference, Dr. Alex Klein
^ Accelerator Technology. doi:10.1007/978-3-030-62308-i.
^ J. Slough, One thousand. Votroubek, and C. Pihl, "Cosmos of a high-temperature plasma through merging and compression of supersonic field reversed configuration plasmoids" Nucl. Fusion 51,053008 (2011).
^ A. Asle Zaeem et al "Aneutronic Fusion in Collision of Oppositely Directed Plasmoids" Plasma Physics Reports, Vol. 44, No. iii, pp. 378–386 (2018).
^ Jones, S.E. (1986). "Muon-Catalysed Fusion Revisited". Nature. 321 (6066): 127–133. Bibcode:1986Natur.321..127J. doi:10.1038/321127a0. S2CID 39819102.
^ Supplementary methods for "Observation of nuclear fusion driven by a pyroelectric crystal". Master article Naranjo, B.; Gimzewski, J.K.; Putterman, S. (2005). "Observation of nuclear fusion driven past a pyroelectric crystal". Nature. 434 (7037): 1115–1117. Bibcode:2005Natur.434.1115N. doi:10.1038/nature03575. PMID 15858570. S2CID 4407334.
^ UCLA Crystal Fusion. Rodan.physics.ucla.edu. Retrieved 17 Baronial 2011. Archived 8 June 2015 at the Wayback Machine
^ Schewe, Phil & Stein, Ben (2005). "Pyrofusion: A Room-Temperature, Palm-Sized Nuclear Fusion Device". Physics News Update. 729 (1). Archived from the original on 12 November 2013.
^ Coming in out of the cold: nuclear fusion, for real. The Christian Science Monitor. (6 June 2005). Retrieved 17 August 2011.
^ Nuclear fusion on the desktop ... really!. MSNBC (27 April 2005). Retrieved 17 August 2011.
^ Naranjo, B.; Putterman, S.; Venhaus, T. (2011). "Pyroelectric fusion using a tritiated target". Nuclear Instruments and Methods in Physics Inquiry Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 632 (1): 43–46. Bibcode:2011NIMPA.632...43N. doi:x.1016/j.nima.2010.08.003.
^ Gerstner, E. (2009). "Nuclear free energy: The hybrid returns". Nature. 460 (7251): 25–28. doi:10.1038/460025a. PMID 19571861.
^ Maugh 2, Thomas. "Physicist is found guilty of misconduct". Los Angeles Times . Retrieved 17 April 2019.
^ FusEdWeb | Fusion Education. Fusedweb.pppl.gov (9 November 1998). Retrieved 17 August 2011. Archived 24 Oct 2007 at the Wayback Machine
^ M. Kikuchi, Grand. Lackner & M. Q. Tran (2012). Fusion Physics. International Atomic Energy Bureau. p. 22. ISBN9789201304100.
^ K. Miyamoto (2005). Plasma Physics and Controlled Nuclear Fusion. Springer-Verlag. ISBN3-540-24217-1.
^ Subsection 4.7.4c Archived xvi August 2018 at the Wayback Machine. Kayelaby.npl.co.uk. Retrieved 19 December 2012.
^ A momentum and energy balance shows that if the tritium has an energy of E_T (and using relative masses of 1, 3, and 4 for the neutron, tritium, and helium) then the energy of the helium can be annihilation from [(12E_T)^i/2−(5×17.6MeV+2×E_T)^1/2]²/25 to [(12E_T)^1/2+(five×17.6MeV+two×E_T)^1/2]²/25. For E_T=1.01 MeV this gives a range from 1.44 MeV to 6.73 MeV.
^ Rider, Todd Harrison (1995). "Cardinal Limitations on Plasma Fusion Systems not in Thermodynamic Equilibrium". Dissertation Abstracts International. 56–07 (Section B): 3820. Bibcode:1995PhDT........45R.
^ Rostoker, Norman; Binderbauer, Michl and Qerushi, Artan. Central limitations on plasma fusion systems not in thermodynamic equilibrium. fusion.ps.uci.edu
^ Huba, J. (2003). "NRL PLASMA FORMULARY" (PDF). MIT Itemize . Retrieved 11 November 2018.
^ Bosch, H. S (1993). "Improved formulas for fusion cross-sections and thermal reactivities". Nuclear Fusion. 32 (4): 611–631. doi:ten.1088/0029-5515/32/4/I07. S2CID 55303621.

External links [edit]

NuclearFiles.org – A repository of documents related to nuclear power.
Annotated bibliography for nuclear fusion from the Alsos Digital Library for Nuclear Issues
NRL Fusion Formulary